Kopiec (Heap)
Kopiec jest strukturą implementowaną jako tablica, ale należy ją traktować jako drzewo binarne. Jest ono zawsze pełne, z wyjątkiem ostatniego poziomu. Kopiec musi spełniać tylko jeden warunek: Dla każdego wierzchołka, jego dzieci muszą być większe. Co oznacza, że korzeń jest najmniejszym elementem kopca. Jak reprezentować drzewo jako tablicę? Pierwszy element tablicy to korzeń. Jego dzieci to drugi i trzeci element. Dzieckiem drugiego elementu jest czwarty i piąty, itd. Widać, że aby znaleźć indeksy dzieci wierzchołka i - tego, wystarczy zastosować wzór (2 * i) dla lewego i (2 * i + 1) dla prawego dziecka. No to jak znaleźć rodzica? Sprawa jest prosta: i / 2 zaokrąglone w dół. Zobaczmy rysunek.
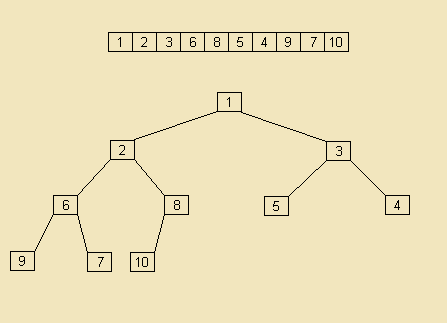
Jest to tablica reprezentująca kopiec i jej odpowiednik w postaci drzewa.
Zanim zajmiemy się szczegółami dotyczącymi kopców jeszcze słówko wyjaśnienia. W C# pracujemy na tablicach indeksowanych od 0. W takim wypadku nasz wzór nie sprawdza się dla korzenia. 0 * 2 = 0, więc jako syna wskażemy jego samego. Modyfikacja jest prosta. Zanim zastosujemy wzór zwiększymy indeks o jeden. Następnie odejmiemy 1 jeśli chcemy znać indeks lewego syna, lub zostawimy w spokoju, jeśli chodzi nam o prawego. Rodzica wyznaczamy podobnie. Najpierw zwiększamy indeks, dzielimy na poł i zmniejszamy. Co się dzieje, gdy wierzchołek nie ma dzieci (lub rodzica w przypadku korzenia)? Zwracamy po prostu -1. Popatrzmy na implementacje tych 3 metod:
private int Parent(int index) {
int parentIndex = (index + 1) / 2;
return parentIndex - 1;
}
private int LeftChild(int index) {
int childIndex = (index + 1) * 2 - 1;
if (childIndex >= this.heapSize)
return -1;
else
return childIndex;
}
private int RightChild(int index) {
int childIndex = (index + 1) * 2;
if (childIndex >= this.heapSize)
return -1;
else
return childIndex;
}
Jeszcze słówko wyjaśnienia, co do pola heapSize. Jest to osobne pole typu int, a nie właściwość Length tablicy dlatego, że musimy mieć większą dowolność w manipulowaniu rozmiarem kopca.
Musimy teraz zdefiniować operacje jakie chcemy wykonywać na kopcu:
- Utwórz kopiec
- Dodaj element do kopca
- Usuń element minimalny
Najpierw zajmiemy się tworzeniem kopca. Do tego przyda się nam pomocnicza metoda DropElement, która sprawdzi, czy dzieci aktualnie sprawdzanego elementu są mniejsze. Jeśli są, to zamieniamy aktualny element z mniejszym dzieckiem i przechodzimy "piętro niżej" postępując podobnie. Kończymy gdy powyższy warunek nie jest spełniony, lub element po prostu nie ma już dzieci.
private void DropElement(int index) {
int leftIndex = LeftChild(index);
int rightIndex = RightChild(index);
int smallerIndex = index;
if (leftIndex == -1)
return;
if (this.heap[leftIndex] < this.heap[index])
smallerIndex = leftIndex;
if (rightIndex != -1 && this.heap[rightIndex] < this.heap[smallerIndex])
smallerIndex = rightIndex;
if (smallerIndex != index) {
Swap(smallerIndex, index);
DropElement(smallerIndex);
}
}
Mamy trzy indeksy. Lewego dziecka, prawego i mniejszego, ustawionego początkowo na aktualny wierzchołek. Na początku sprawdzamy, czy są dzieci. Wystarczy, że sprawdzimy tylko lewe, bo jak nie ma lewego dziecka, to prawego też nie będzie. Później wyznaczamy najmniejszy element z całej trójki i jeśli nie jest on korzeniem, to go z nim zamieniamy i schodzimy w dół. Teraz możemy przejść do właściwego budowania kopca.
Zauważmy, że od połowy w dół, mamy dobrze utworzone kopce 1 - elementowe. Wykorzystamy ten fakt. Tak więc na pozycji (n / 2) - 1 jest rodzic dwóch ostatnich elementów (lub jednego). No to zbudujmy kopiec większy poprzez wywołanie metody DropElement na tym wierzchołku. Wszyscy się na pewno zgodzą, że powstanie dzięki temu większy, dobrze zdefiniowany kopiec. No to teraz powtórzmy to samo dla kolejnych elementów. Gdy dojedziemy już do pierwszego elementu, utworzony zostanie kopiec składający się ze wszystkich elementów tablicy. Na pierwszy rzut oka, budowanie kopca trwa O(n * logn), ale po głębszej analizie, wyjdzie, że trwa to w czasie liniowym. To okaże się ważne przy sortowaniu przez kopcowanie. Zobaczmy na rysunku jak działa budowanie kopca.
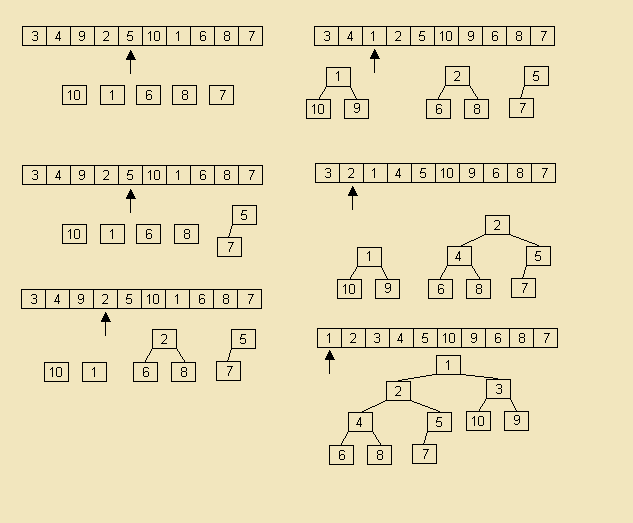
Widzimy tablicę i odpowiadające jej rysunki kopców. Zaprezentuję teraz niezwykle skomplikowaną implementację budowy kopca, a następnie zobaczymy pozostałe operacje, jakie można wykonywać na kopcu.
private void BuildHeap() {
for (int k = this.heapSize / 2 - 1; k >= 0; k--)
DropElement(k);
}
Usuwanie elementu minimalnego z kopca. Naprawdę prosta operacja. Wiemy, że element minimalny jest w korzeniu, ale trzeba jeszcze przywrócić porządek kopca po jego usunięciu. Pomysł jest taki, żeby zamienić pierwszy element w tablicy z ostatnim. Zmniejszamy teraz rozmiar kopca i wywołujemy metodę DropElement(0). Dzięki temu porządek kopca zostanie zachowany, a element minimalny usunięty. Zwykle metoda musi jeszcze zwrócić usuwany element, ale to nie problem. Spójrzmy na kod źródłowy:
public int DeleteMin() {
if (this.HeapSize == 0)
return -1;
Swap(0, this.HeapSize - 1);
this.heapSize--;
DropElement(0);
return this.heap[this.heapSize];
}
No to jeszcze wstawianie elementu. Tu również nie ma żadnej filozofii. Wstawiamy nowy element na końcu tablicy (zwiększając przy tym rozmiar). Szukamy rodzica tego elementu. Sprawdzamy, czy jest mniejszy od rodzica. Jeśli tak, to zamieniamy oba elementy i sprawdzamy wyżej. Jeśli nie, to znaczy, że kopiec jest OK.
public void InsertElement(int element) {
if (this.heapSize >= this.heap.Length)
ResizeHeap();
this.heap[this.heapSize] = element;
int elementIndex = this.heapSize;
this.heapSize++;
while (Parent(elementIndex) != -1 && this.heap[elementIndex] < this.heap[Parent(elementIndex)]) {
Swap(elementIndex, Parent(elementIndex));
elementIndex = Parent(elementIndex);
}
}
Słowo wyjaśnienia co do tego magicznego "ResizeHeap". To nie ma nic wspólnego z samym algorytmem, lecz służy do wydłużenia tablicy jeśli jest za krótka. Cała reszta powinna być jasna. Mając teraz wiedzę na temat kopców zapraszam do zapoznania się z algorytmem sortowania przez kopcowanie.



